Final Summary Martin Leonardo Hermawan 2301873043

Linked List

Linked list atau senarai berantai adalah sebuah struktur data yang digunakan untuk meyimpan sejumlah objek data biasanya secara terurut sehingga operasi penambahan, pengurangan, dan pencari data yang tersimpan dapat dilakukan dengan lebih mudah tentunya lebih cepat.

Pada saat ini, saya akan membahas 3 macam linked list yaitu :

• Circular single linked list
• Doubly linked list
• Circular doubly linked list

Circular Single Linked List

Circular linked list adalah single linked list, namun pada circular single linked list tail/pointer terakhir dari linked list tersebut tidak bernilai null melainkan menunjuk ke head/pointer awal dari linked list itu. Karena itu, jika kita lihat, circular single linked list berbentuk seperti single linked list yang diakhiri dengan loop ke awal. Gambarnya seperti berikut.

Doubly Linked List

Doubly linked list adalah linked list dengan node yang memili 2 buah reference link dan sebuah data. Reference link tersebut menunjuk ke node sebelum dan node sesudahnya.

Doubly linked list memiliki beberapa operasi dasar seperti:

• Insert First: penyisipan di awal list, pointer head akan berpindah ke elemen baru
• Insert Last : penyisipan di akhir list, pointer tail akan berpindah ke elemen baru
• Insert After/Before : penyisipan sesudah/sebelum 
• Delete First: penghapusan di awal list, pointer head akan berpindah ke node selanjutnya
• Delete Last: penghapusan di akhir list, pointer tail akan berpindah ke node sebelumnya
• Delete Node: penghapusan node tertentu

Gambarnya seperti berikut.

Circular Doubly Linked List

Circular doubly linked list adalah seperti doubly linked list. Pada circular doubly linked list, node paling akhir/tail memiliki reference link yang menunjuk ke head/node awal. Oleh karena itu, circular doubly linked list adalah doubly linked list yang memiliki loop dari node terakhir ke awal.

Gambarnya seperti berikut.

Sekian penjelasan saya mengenai  circular single linked list, doubly linked list, dan circular doubly linked list. Semoga penjelasan saya dapat dengan mudah dimengerti. Terimakasih

Referensi gambar:

https://www.studytonight.com/data-structures/circular-linked-list

https://www.geeksforgeeks.org/doubly-linked-list/

https://www.geeksforgeeks.org/doubly-circular-linked-list-set-1-introduction-and-insertion/

Hashing Table & Binary Tree

Hashing

Hashing berasal dari kata hash yaitu suatu kode hasil enkripsi yang biasanya terdiri atas huruf ataupun angka yang acak. Hash berfungsi untuk mempercepat pencarian data misalnya dalam sebuah tabel data. Oleh karena itu, hashing digunakan untuk menyimpan data dalam sebuah array sehingga proses prnyimpanan, pencarian, penambahan, dan penghapusan data dapat dilakukan dengan cepat. Hashing juga dapat dikatakan transformasi aritmatik sebuah string karakter menjadi nilai yang merepresentasikan string aslinya. Ide dasar hashing adalah menghitung posisi record yang dicari dalam array. Fungsi yang digunakan adalah fungsi hash atau biasa disebut hash function. Array yang digunakan dalam hasing disebut hash table yang menggunakan struktur data array asosiatif yang mengasosiasikan record dengan sebuah field kunci unik berupa bilangan (hash) yang merupakan representasi dari record tersebut.

Fungsi hash menyimpan nilai asli atau kunci pada alamat yang sama dengan nilai hashnya. Pertama, akan dilakukan penghitungan nilai hash dari kuncinya. Lalu, kunci dibandingkan dengan isi pada memori yang beralamatkan nomor hashnya. Oleh karena itu, fungsi ini dapat berjalan dengan cepat.

Hashing sangat berguna dalam blockchain, hash sangat berguna dalam memecahkan data yang terenkripsu untuk menyelesaikan perhitungan blockchain. Hash memiliki panjang yang tetap karena tidak mungkin seseorang menebak panjang hash untuk memecahkan blockchain.

Ada beberapa cara untuk mengubah string menjadi key dalam fungsi hash. Berikut beberapa caranya.

1. Division

     Menggunakan modulus sebesar ukuran array.

h(k) = k mod n

k=1276
n=10
h(1276) = 1276 mod 10
           = 6

2. Multiplication

     h(k) = floor( n( kA mod 1 ) )

k=123
n=100
A=0.618033
h(123) = 100 (123 * 0.618033 mod 1)
           =  100 (76.018059 mod 1)
           =  100 (0.018059)
           =   1

3. Mid Square

Hash table adalah sebuah struktur data yang memetakan kunci untuk sebuah nilai.

Berikut contohnya.

35  50  11  79  76  85

Kita memakai fungsi h(k) = k mod 10

4. Folding
     String/identifier dipartisi menjadi beberapa bagian, lalu bagian-bagian ditambahkan bersama untuk mendapatkan kuncinya.

5. Digit Extraction
     Sebuah digit yang ditentukan sebelumnya dari sebuah nomor dianggap sebagai alamat hash.
     Contoh : misalkan x = 16273
                    jika kita mengambil digit ke 1, 3, dan 5, kita akan dapat kode hashnya yaitu 123.

6. Rotating Hash
     Awalnya kita gunakan method yang lain. Lalu, setelah dapat kodenya kita lakukan rotation. Rotation memutarbalikan kode yang sudah ada. Misalkan kodenya 28173 menjadi 37182.

Collision
Tabrakan antara kunci hash , dimana ada record yang memiliki kunci ayng sama.
Ada 2 cara untuk menyelesaikan collision yaitu:
1. Linear Probing : mencari slot kosong berikutnya dan menyimpan stringnya disana.
2. Chaining : menyimpan setiap string dalam sebuah rantai (linked list).

Binary Tree

Binary tree adalah sebuah pohon struktur data dimana setiap simpul/node memiliki paling banyak dua cabang. Biasanya cabang disebut kiri dan kanan.

Ada 4 jenis binary tree, yaitu :

1. Perfect binary tree : binary tree dimana tiap level berada pada kedalaman yang sama

2. Complete binary tree : binary tree dimana tiap level semuanya terisi kecuali biasanya yang terakhir dan biasanya semua node berada di kiri.

3. Skewed binary tree : binary tree dimana setiap node paling banyak memiliki 1 cabang/anak

4. Balanced binary tree : binary tree dimana tidak ada daun yang lebih jauh dari akar daripada daun lainnya.

Property of Binary Tree

• Jumlah maksimum setiap node pada level k adalah 2^k
  

• Jumlah maksimum node dalam sebuah binary tree sebanyak h level adalah (2)^h+1 -1
• Tinggi sebuah tree adalah jumlah level yang ada (tidak termasuk akarnya) atau level tertingginya.
• Tinggi minimum sebuah pohon biner yang terdiri atas n node adalah 2log(n)
• Tinggi maksimum sebuah pohon biner yang terdiri dari n node adalah n-1

Representation of Binary Tree

• Implementation using linked list

           struct node {

                     int data;

                     struct node *left;

                     struct node *right;

                     struct node *parent;

           };

           struct node *root = NULL;

Expression Tree Concept

Prefix : *+ab/-cde

Postfix : ab+cd-e/*

Infix : (a+b)*((c-d)/e)

Prefix

Main function : struct tnode *root = newnode(s[0]);

                          f(root);

char s[MAXN];int  p = 0;void f(struct tnode *curr) {  if ( is_operator(s[p]) ) {  p++; curr->left  = newnode(s[p]);  f(curr->left);  p++; curr->right = newnode(s[p]);  f(curr->right);  }

}

void prefix(struct tnode *curr) {

  printf( “%c “, curr->chr );

  if ( curr->left  != 0 ) prefix(curr->left);

  if ( curr->right != 0 ) prefix(curr->right);
}

Dalam Prefix, kita harus print/proses sebelum child diproses

Postfix

void postfix(struct tnode *curr) {

    if ( curr->left  != 0 ) postfix(curr->left);

    if ( curr->right != 0 ) postfix(curr->right);
    printf( “%c“, curr->chr );

}

Dalam Postfix, kita harus print/proses setelah child diproses

Infix

Prefix  : *+abc

Postfix  : ab+c*

Wrong infix  : a+b*c

Correct infix  : (a+b)*c

void infix(tnode *curr) {

    if ( is_operator(curr->chr) ) putchar( '(' );

    if ( curr->left != 0 ) infix(curr->left);

    printf( "%c", curr->chr );

    if ( curr->right != 0 ) infix(curr->right);

    if ( is_operator(curr->chr) ) putchar( ')' );

}

Threaded Binary Tree Conecpt

Threaded binary tree sebenarnya sama dengan binary tree hanya berbeda dalam menyimpan pointer NULL.

Ada 2 jenis threaded binary tree, yaitu :

1. One Way Threading
   
   
   

     2. Two Way Threading

AVL Tree

AVL Tree adalah sebuah BST (Binary Search Tree) yang memiliki maksimal perbedaan tinggi level 1 antara subtree kiri dan subtree kanan. AVL Tree berguna untuk menyeimbangkan BST. Waktu pencarian yang dibutuhkan lebih sedikit dan bentuk tree akan terlihat lebih sederhana.

Contoh AVL Tree

Contoh yang bukan AVL Tree

Dapat dilihat subtree kiri dari node 76 ada 3 tetapi subtree kanannya 0 jadi perbedaan tinggi nya 3.

Insertion

Ada 4 kasus dalm insertion, yaitu :

• Jika ada ketidakseimbangan pada anak kiri subtree kanan, maka dilakukan rotasi kiri-kanan.
• Jika ada ketidakseimbangan pada anak kiri subtree kiri, maka dilakukan rotasi kanan.
• Jika ada ketidakseimbangan pada anak kanan subtree kanan, maka dilakukan rotasi kiri.
• Jika ada ketidakseimbangan pada anak kanan subtree kiri, maka dilakukan rotasi kanan-kiri.

Untuk menjaga tree tetap seimbang, setelah penambahan sebuah node, dilakukan pemeriksaan dari node baru ke root. Node pertama yang memiiki balance factor > 1 diseimbangkan. Proses penyeimbangan dilakukan dengan 2 cara yaitu single rotation dan double rotation.

Single Rotation

Double Rotation

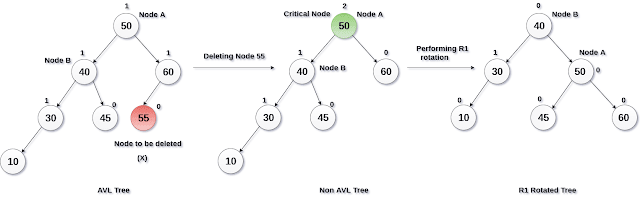
Deletion

Proses menghapus sebuah node AVL Tree hampir sama dengan BST. Penghapusan sebuah node dapat membuat sebuah tree menyadi tidak seimbang. Setelah menghapus sebuah node, lakukan pengecekan dari node yang dihapus ke root. Gunakan single rotation atau double rotation untuk menyeimbangkan node yang tidak imbang.

Heap

Heap adalah struktur data berbasis tree dimana tree itu adalah complete binary tree. Secara umum, ada 2 jenis heap yaitu:

1. Max Heap : kunci yang ada di simpul akar harus paling besar diantara kunci yang ada d semua anak-anak itu. Properti yang sama harus benar secara rekursif untuk semua subtree di binary tree tersebut.
   
2. Min Heap : kunci yang ada di simpul akar harus minimum diantara kunci yang ada di semua anak-anak itu. Properti yang sama harus benar secara rekursif untuk semua subtree di binary tree tersebut.
   

Selain 2 heap diatas ada juga max-min heap yaitu complete binary tree yang berisi level min (atau genap) dan maks (atau ganjul) secara bergantian. Level genap dilambangkan seperti 0, 2, 4, dll, dan level ganjil dilambangkan dengan 1, 3, 5, dll. Berikut ini contohnya

Insertion

Pertama, meningkatkan ukuran heap oleh 1, sehingga dapat menyimpan elemen baru. Masukkan elemen baru di akhir heap. Elemen yang baru diinsert ini dapat merusak heap. Jadi, untuk menjaga heap, dilakukan heapify elemen yang baru diinsert dengan cara bottom-up.

Illustration:

Suppose the Heap is a Max-Heap as:
      10
    /    \
   5      3
  / \
 2   4

The new element to be inserted is 15.

Process:
Step 1: Insert the new element at the end.
      10
    /    \
   5      3
  / \    /
 2   4  15

Step 2: Heapify the new element following bottom-up 
        approach.
-> 15 is more than its parent 3, swap them.
       10
    /    \
   5      15
  / \    /
 2   4  3

-> 15 is again more than its parent 10, swap them.
       15
    /    \
   5      10
  / \    /
 2   4  3

Therefore, the final heap after insertion is:
       15
    /    \
   5      10
  / \    /
 2   4  3

Deletion

Ganti root atau elemen yang akan dihapus oleh elemen terakhir. Hapus elemen terakhir dari heap. Karena, elemen terakhir sekarang ditempatkan pada posisi node root. Jadi, mungkin tidak mengikuti properti heap. Oleh karena itu, heapify simpul terakhir yang ditempatkan di posisi root.

Illustration:

Suppose the Heap is a Max-Heap as:
      10
    /    \
   5      3
  / \
 2   4

The element to be deleted is root, i.e. 10.

Process:
The last element is 4.

Step 1: Replace the last element with root, and delete it.
      4
    /    \
   5      3
  / 
 2   

Step 2: Heapify root.
Final Heap:
      5
    /    \
   4      3
  / 
 2   

Tries

Trie adalah struktur data pencarian yang efisien. Kompleksitas pencarian dapat dilakukan dengan bata optimal (panjang key). Jika kita menyimpan kunci dalam binary search tree, binary seach tree yang seimbang akan membutuhkan waktu yang sama dengan  M * log N, dimana M adalah panjang string maksimum dan N adalah jumlah key dalam tree. Dengan menggunakan trie, kita dapat mencari key dalam waktu O(M). Namun, ada persyaratan penyimpanan trie. Setiap simpul trie terdiri dari banyak cabang. Setiap cabang mewakili karakter key yang memungkinkan. Kita perlu menandai simpul terakhir dari setiap key sebagai simpul kata terakhir. Bidang simpul isEndOfWord digunakan untuk membedakan simpul tersebut sebagai simpul akhir kata.